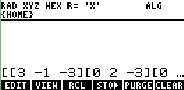|
Miscellaneous |
|
Miscelaneous
Including: Vectors, HYP Functions, Complex & Real Numbers.
Vectors
1) ABS
Calculates the norm of a vectror
The norm of a vector [ a b c ] is definite as SQRT(a^2 + b^2 + c^2)
Example:
Find the norm of the vector [2 3 4]
level 1: [2 3 4]
[MTH][VECTR][ABS]
Result: 5.38516480713
2) DOT
Calculates the scalar product of two vectors.
The result is a number.
Example:
[2 3 4].[6 7 8]
level 2: [2 3 4]
level 1: [6 7 8]
[MTH][VECTR][DOT]
Result: 65
3) CROSS
Calculates the vectorial produc of two vectors.
The result is a vector.
Example:
[2 3 4] x [6 7 8]
level 2: [2 3 4]
level 1:[6 7 8]
[MTH][VECTR][CROSS]
Result: [-4 8 -4]
4)  V2
V2
Convert numbers in levels 1 and 2 into a vector.
Example:
level 2: 9
level 1: 8
[MTH][VECTR][ V2]
V2]
Result: [9 8]
5)  V3
V3
Convert numbers in levels 1, 2 and 3 into a vector.
Example:
level 3: 4
level 2: 5
level 1: 8
[MTH][VECTR][ V3]
V3]
Result: [4 5 8]
6) V
Re-convert a vector into stack numbers.
Example:
level 1:[2 6 1 ]
[MTH][VECTR][V ]
]
Result:
level 3: 2
level 2: 6
level 1: 1
Hyperbolic Functions
Hyperbolic functions are functions based on exp(x)
To find the value of an hyperbolic trigonometric
funtion all you need is to put the number
on the stack and press the respective function at [MTH][HYP]
Example:
Calculate the sinh(5)
level 1: 5
[MTH][HYPER][SINH]
Result: 74.2032105778
Real & Complexes Numbers
In HP 48 complexes numbers are represented between ( ).
as (real part, complex part)
Work with complexes numbers in HP48 is easy.
Below are listed the most useful functions.
1) RE
Returns the real part of a complex number
Example:
Find the real part of (123, 456)
Level 1: (123, 456)
Press [MTH][NXT][CMPL][RE]
Result: 123
2) IM
Returns the imaginary part of a complex number
Example:
Find the imaginary part of (123, 456)
Level 1: (123, 456)
Press [MTH][NXT][CMPL][IM]
Result: 456
3) ABS
Returns the norma of a complex number
Example:
Find the real part of (123, 456)
Level 1: (123, 456)
Press [MTH][NXT][CMPL][ABS]
Result: 472.297575687
4) ARG
Return the angle argument of a complex number
Example:
Find the angle argument of (123, 456)
Level 1: (123, 456)
Press [MTH][NXT][CMPL][ARG]
Result:
74.9044791558 (angle mode)
1.30732978576 (rad mode)
5) CONJ
Return the conjugate of a complex number
Example:
Find the angle conjugate of (123, 456)
Level 1: (123, 456)
Press [MTH][NXT][CMPL][ARG]
Result: (123, -456)
Real Numbers
1) RND
Rounds a number for a definite numbers of digits
Level 2:
1.8678987
Level 1:
3
Press
[MTH][REAL][RDN]
Result: 1.868
2) TRNC
Truncates a number to the set numbers of digits
Level 2:
1.8678987
Level 1:
3
Press
[MTH][REAL][TRNC]
Result: 1.867
3) MOD
Returns the rest of a division between two numbers
Example:
Level 2:
14
Level 1:
3
Press
[MTH][REAL][MOD]
Result: 2
Note: 8 / 3 = 4 and rest 2.
4) IP
Show the Integer Part of a number
Example:
Level 2:
1.8678987
Press
[MTH][REAL][IP]
Result: 1
5) FP
Show the Fraction Part of a number
Example
Level 2:
1.8678987
Press
[MTH][REAL][FP]
Result:. 8678987
6) D R
R
Converts from Degree to radians
Example
Level 2:
45
Press
[MTH][REAL][D R]
R]
Result:
.785398163397
7) R D
D
Converts from Radians to Degree
Example
Level 2:
.785398163397 Example
Press
[MTH][REAL][R D]
Result: 45
8) CEIL
D]
Result: 45
8) CEIL
Returns the mayor integer closest to the number
Example
Level 2:
1,45
Press
[MTH][REAL][CEIL]
Result: 2
9) FLOOR
Returns the minor integer closest to the number
Example
Level 2:
1,45
Press
[MTH][REAL][FLOOR]
Result: 1
10) %
Returns the percentage
Example
Level 2:
100
Level 1:
12,67
Press
[MTH][REAL][%]
Result:12.67
Eigenvectors and Eigenvalues
1) EGV
The command
EGV calculates the
eigenvalues and the
eigenvectors of a given matrix.
Example
Claculates the eigenvalues and the eigenvectors of the matrix
 Resolution:
Resolution:
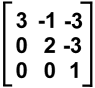
1- write the matrix in the HP48/49 as below
and press
[ENTER]
2- type
EGV and press
[ENTER]
It will show:
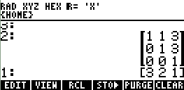
where the columns of the matrix are the eigenvectors associated
to the eigenvalues shown in the vector below the matrix.
In this example,
[1 0 0] is the eigenvector associated to
3
[1 1 0] is the eigenvector associated to
2
[3 3 1] is the eigenvector associated to
1
2) EGVL
The command
EGVL calculate the eigenvector of a given matrix
Example
Claculates the eigenvalues and the eigenvectors of the matrix
 Resolution:
Resolution:
1- write the matrix in the HP48/49 as below
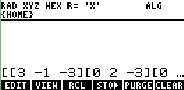
and press
[ENTER]
2- type
EGVL and press
[ENTER]
it shows the vector
[ 3 2 1]
where
3,
2 and
1 are the eigenvalues for the matrix.
Note:
These examples was done with
HP49 mode set RPN
HP48 is also able to calculate eigenvalues and eigenvectors,
but HP48 shows the eigenvector matrix in line,
and eigenvalues as a vector.
For the examples of
EGV above it shows something like,
[ [ 1 1 3 ] [ 0 1 3 ] [ 0 0 1] ]
[ 3 2 1].
Press
[SWAP] to see it like.
[ 3 2 1]
[ [ 1 1 3 ]
[ 0 1 3 ]
[ 0 0 1 ] ]
Where the eigenvectors are shown as colums of the matrix,
and the eigenvalues as the vector
[ 3 2 1].
Back to Top
End of File
 V2
V2 V2]
V2] V3
V3 V3]
V3]
 ]
]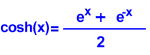
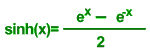
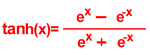
 R
R  R]
R]  D
D D]
D]