Traducido del original de
Carlos Marangon
por Emiterio Burga Uriarte, desde Peru en abril
de 2000
1-Definiciones
Tutorial de integrales
Es una entidad matematica usada para calcular areas,volumenes,longitudes,centroides,etc.
Un integral es aplicable a una función continua en un intervalo definido de la variable de la función
| Se
reprecenta por el simbolo |
Integral Definida
| La expresión
representada por |
Las integrales definidas se utilizan para calcular, en general, valores numéricos de áreas, volúmenes, centroides, longitudes, etc. Puede ser comparado a la suma de todos los elementos del área de ancho dx y de altura y=f(x) de un diagrama de la función. Cuando el dx tiende a cero el número de elementos tiende a infinito y a la suma sera más perfecta, dando la mejor precisión al cálculo.
| Una integral puede ser estimada sumandose todos los elementos de anchura dx y de altura y=f(x). El resultado de esta operacción es más próximo al verdadero valor de la integral cuanto menor sea el diferencial dx, y consecuentemente más grande el número de elementos de area así como el tiempo tomado para realizar el cálculo. En la ilustración a y b son los límites de la integración, las líneas del color son los elementos de area, dx la longitud de los elementos del área y f(x) la altura del elemento del área. |
La suma de un numero finito de elementos de altura y=f(x) y ancho dx para estimar la Integral |
Integral Indifinida
| La expresion
reprecentada como |
| El cálculo de una integral indefinida es básicamente encontrar otra función llamada antiderivada, que resulta derivando el resultado de la integracion de f(x). |
La derivda de una antiderivada es igual a la integracion de f(x) |
Para los usuarios de la HP48 usualmente se llama INTEGRAL SIMBOLICA.
Sin embargo,el termino integral simbolica no es aplicado en la comunidad matematica.
| Nombre dado a las
expresiones representadas como |
2-Usando la HP48 para resolver Integrales
Nota: check los flags -01,-02 y -03
antes de intentar resolver una integral.
Deben ser fijados según el resultado que usted desea, simbólico
o numérico.
integrales Indefinidas
HP48 no puede solucionar todas las clases de integrales indefinidas. Por favor, vea la paginación 20-8 de la guía del usuario para más información. Los graficos de pantalla de abajo muestran el resultado para una función que no pudo integrace y otra función que fue integrada.
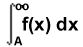 Aplicacion de solve Integrate |
 Muestra un resultado, como esto, cuando no soluciona la integral |
 Aplicacion de solve Integrate |
 Muestra un resultado, como esto, cuando soluciona la integral |
Para solucionar una integral indefinida todo lo que necesitamos ejecutar es;
 |
|
| Ingresar
la EXPR , VAR, LO y HI. fijar el resultado como SYMBOLIC y presionar OK en el menu. |
 |
| Nota: Ud tambien puede solucionar integrales usando el escritor de ecuaciones(EQUATION WRITER )y presionar EVAL cuando finalice de escribir la expresion. |
 Escriniendo la integral en el EQUATION WRITER |
Integrales Definidas
La serie HP48 G puede solucionar todas los integrales definidas y toma más o menos un tiempo solucionarlas, según la precisión del cálculo.
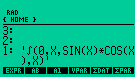
Para solucionar una integral definida todo lo que necesitamos es ejecutar;
 |
|
| Ingresar
la EXPR , VAR, LO y HI. fijar el resultado como NUMERIC y presionar OK en el menu. |
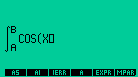 |
| Nota: Ud tambien puede solucionar integrales usando EQUATION WRITER y presionar EVAL cuando finalice de escribir la expresion.. |
 Escribiendo la integral en el EQUATION WRITER |
Acelerando la integracion numerica
La serie HP48 G permite solucionar
mas rapido.
Definiendo el numero de digitos decimales es posible hacer que la
calculadora solucione las integrales
más rápido que al usar el valor completo de 12 dígito.
| Para
acelerar el calculo es necesario definir el numero de
digitos decimalesusando la funcion FIX.Puede ser 3 FIX, 5 FIX o 8 FIX de acuerdo a la precision. |
|
Tabla de resultados de los calculos
| Vamos
a integrar f(X)=sin(X) con X desde 0 a 50 |
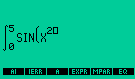 |
La HP48 devuelve los siguientes
resultados de acuerdo a la precision
y el tiempo en solucionar la integral.
| FIXED FORMAT | RESULT | TIME TO SOLVE | DIFFERENCE* |
| 1 FIX | 0.1 | 2s | -6.50 E -2 |
| 2 FIX | 0.03 | 3 s | 5.03 E -3 |
| 3 FIX | 0.035 | 4 s | 3.40 E -5 |
| 4 FIX | 0.0350 | 6 s | 3.40 E -5 |
| 5 FIX | 0.03503 | 6 s | 3.97 E -6 |
| 6 FIX | 0.035034 | 7 s | -2.80 E -8 |
| 7 FIX | 0.0350340 | 11 s | -2.80 E -8 |
| 8 FIX | 0.03503397 | 12 s | 1.52 E -9 |
| 9 FIX | 0.035033971 | 22 s | 5.16 E -10 |
| 10 FIX | 0.0350339715 | 23 s | 1.60 E -11 |
| 11 FIX | 0.03503397152 | 44 s | 4.00 E -12 |
| STD | 0.035033971516 | 46 s | 0.00 E 0 |
*La diferencia mostrada en la cuarta columna es el valor que conseguimos cuando reste el resultado del formato fijo respectivo del valor calculado con lal HP48 trabajando en el modo más exacto, es decir en el modo del STD.
Como podemos ver en la fila amarilla, el resultado para HP48 que trabaja en el ARREGLO del formato fijo 5, es un buen resultado. Podemos concluirlo que el uso de 5 digitos es satisfactorio para solucionar integrales numéricas.
Integrales Impropias
La HP48 puede solucionar
integrales impropias,pero antes hay que hacer un reemplazo de
variable preliminar.
Asegurese de que la integral impropia sea convergente o la
calculadora le devolvera un valor absurdo ademas de la cantidad
de tiemo que tomara.
por ejemplo:
| Si tuvieranos la siguiente integral impropia y nos piden integral desde x:1 --> infinito |  |
Un cálculo preliminar es
necesario para substituir variables
Vamos a hacer un cambio de variable
Hacemos que X = tan(Y) .
1- haciendo X = tan(Y)
2- remplazando dx por dy
dX/dY = d(tan(Y))/dY que resulta dX
= (1+ tan2(Y)) dY
3- reemplazando la funcion f(X)
= f(tan(Y)) ;
por la funcion f(X)=1/(X2+5X+2) tenemos
f(tan(Y))
= 1/( tan2(Y) + 5. tan(Y) +2)
4-remplazando los limites
Tenemos X=1 como limite inferior y X=¥ como superior.
pero como a X es ahora X=tan(Y)
Tambien
1=tan(y), despejando Y tenemos Y=atan(1)
y
¥=tan(y),despejando Y tenemos Y=atan(¥ ),
que en la sintaxis de la HP48 se puede escribir como Y=atan(MAXR)
Nota:
Recuerde que en la HP48 - ¥ no es MINR (1E- 499) si no -MINR (-1E-499).
En resumen..
| Cuando en la funcion original tenga | necesitamos cambiar por |
| limite inferior | atan(limite inferior) |
| limite superior | atan(limite superior) |
| ¥ | atan(MAXR) |
| - ¥ | atan(-MAXR) |
| X | tan(Y) |
| dx | (1+ tan2(Y)) dY |
Estos reemplazos son válidos para la mayor parte de las integrales impropias.
Remplazando en la formula
| Ahora podemos sustituir las expresiones en la formula: |  |
|
| 1-remplazando los limites ¥ por atan(MAXR) y 1 por atan(1) |
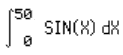 |
|
| 2-remplazando x por tan(y) | 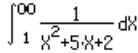 |
|
| 3-remplazando dx por (1+tan(y)2) | 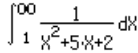 |
|
Intenta reemplazar expresiones con
la tabla de arriva para mas ejemplos de integralesa impropias
en tu libro de calculo integrales y checa los resultados
Resolviendo Integrales Impropias en la calculadora HP48G Series.
| Ahora
necesitamos escribir la integral
|
La expresion completa en pantalla |
| y presionar EVAL para obtener el resultado. |
Resultado de la integral |
Resolviendo Integrales Dobles y Triples
Los pasos para solucionar una
integral doble o triple no son dificultosos
es basicamente solucionar una integral 2 0 3 veces .
Todo lo que necesita es escribir la expresion en el EQUATION WRITER
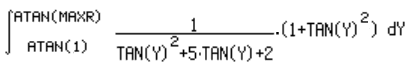 Escribiendo una integral doble. |
Escribiendo una integral triple |
y presiona EVAL pra solucionarlo.
Ejercicios
Use la HP48 y los metodos expuestos en este documento pra solucionar las siguentes integrales:
| Integral to solve | Result |
| a)
|
2/3 or 0.66666666666 |
| b)
|
1/78635793761 or 1.27168551644E-11 |
| c)
|
1/16 or 0.0625 |
| d)
|
4/3 or 1.33333333333 |
| e)
|
|
| f)
|
p/2 or 1,5707963268 |
| g)
|
1/6 or 0.166666666666 |
| h)
|
- ( 1/6*A^6+A^2 +3*A) + (1/6*B^6 +B^2 +3*B) |
| i)
|
-SIN(R) + SIN(S) |
Copyrights:
Original en Ingles:Carlos
Marangon Jan 1999
http://www.area48.com/integral
Traducido por Emiterio Burga Uriarte
Este documento puede ser copiado y distribuido libremente solo
con fines educativos
Esta prohibida su reproduccion con fines no educativos.
Puede ser publicado en sitios de la www siempre y cuando mantenga
el nombre del autor.
Derechos
Reservados © abril 2000.
http://www.geocities.com/adictoshp/integrales.html
hpcodex@yahoo.com