Integrals

The Integrals Help Document
By Carlos Marangon Jan, 20 1999

Definite integrals are used to calculate, in general, numeric values of areas, volumes, centroids,
lengths, etc. It can be compared to the sum of all the elements of area of width dx and of height
y=f(x) of a function plot. When dx tends to zero the number of elements tends to infinite and the
sum more perfect, giving bes MINR (1E- 499) neither -MINR (-1E-499).

To be accurate...

When in the Original Function we have	we need replace for
lower limit	atan(lower limit)
upper limit	atan(upper limit)
¥	atan(MAXR)
- ¥	atan(-MAXR)
X	tan(Y)
dx	(1+ tan2(Y)) dY

These replacements work for the greatest part of improper integrals.

Replacing in the Formula

Now we are able to replace the expressions in the formula
1-replacing the limits ¥ for atan(MAXR) and 1 for atan(1)
2-replacing f(x) for tan(x)
3-replacing dx for (1+tan(x)2)

Try use the replacement expressions in the table above for more examples of improper you have
in your book of calculus integrals and check the result.

Now all we need is write the integral in the EQUATION WRITER	Long screenshot of the expression
and press EVAL to get the result.	Result of the integral

Writing a Double Integral

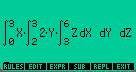Writing a Triple Integral

Exercises

Use HP48 and the methods explained in this document to solve the following integrals:

Transfer interrupted!

Note: You can also solve integrals using the EQUATION WRITER and pressing EVAL when finish writing the expression.

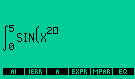Writing the integral in the EQUATION WRITER

Speeding the Numeric Integration

HP48 G series permits speed the time of integration, in spense of the precision
of the calculus. Defining the number of decimal digits it is possible to make the
calculator solve integrals faster than when using the full 12 digits value.

To speed the calculation it is needed define the number of decimal digits using the function FIX. It can be set usually 3 FIX, 5 FIX or 8 FIX according to the precision.

Table of results of Calculations

Lets integrate f(X)=sin(X) on the variable X form 0 to 50

HP48 returns the following values according to the precision
and times to solve an integral.

FIXED FORMAT	RESULT	TIME TO SOLVE	DIFFERENCE*
1 FIX	0.1	2s	-6.50 E -2
2 FIX	0.03	3 s	5.03 E -3
3 FIX	0.035	4 s	3.40 E -5
4 FIX	0.0350	6 s	3.40 E -5
5 FIX	0.03503	6 s	3.97 E -6
6 FIX	0.035034	7 s	-2.80 E -8
7 FIX	0.0350340	11 s	-2.80 E -8
8 FIX	0.03503397	12 s	1.52 E -9
9 FIX	0.035033971	22 s	5.16 E -10
10 FIX	0.0350339715	23 s	1.60 E -11
11 FIX	0.03503397152	44 s	4.00 E -12
STD	0.035033971516	46 s	0.00 E 0

* The difference shown in the fourth column is the value we get when subtract the result of the respective fixed format from the value
calculated with the HP48 working in the most precise mode , i.e. in the STD mode.

As we can see in the yellow row, the result for HP48 working at the fixed format 5 FIX,
is a good result. So we can conclude it is satisfactory use 5 FIX to solve numeric integrals.

Improper Integrals

HP48 can solve improper integrals, but it needs a preliminar variable replacement.
Be sure the improper integral converges before integrate, or it will return an absurd
value and takes much time.

For example:

Lets integrate the function besides, on the variable X, from 1 to infinity

A preliminary calculus is necessary in order to replace variables.
Lets use of an mathematical shotcut to replace the variable.

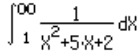Lets make X = tan(Y) and calculate.

1- making X = tan(Y)

2- replacing dx for dy
dX/dY = d(tan(Y))/dY that results dX = (1+ tan²(Y)) dY

3- replacing the function f(X) = f(tan(Y)) ;
for the function f(X)=1/(X²+5X+2) we have f(tan(Y)) = 1/( tan²(Y) + 5. tan(Y) +2)

4-replacing the limits
We have X=1 as lower limit and X=¥ as upper limit.
from the replacement formula we know that X=tan(Y)

so
1=tan(y), isolating Y we have Y=atan(1)
and
¥=tan(y),isolating Y we have Y=atan(¥ ),
that in HP48 syntax can be written as Y=atan(MAXR)

Note:
Remember that in HP48 - ¥ is not MINR (1E- 499) neither -MINR (-1E-499).

To be accurate...

When in the Original Function we have	we need replace for
lower limit	atan(lower limit)
upper limit	atan(upper limit)
¥	atan(MAXR)
- ¥	atan(-MAXR)
X	tan(Y)
dx	(1+ tan2(Y)) dY

These replacements work for the greatest part of improper integrals.

Replacing in the Formula

Now we are able to replace the expressions in the formula
1-replacing the limits ¥ for atan(MAXR) and 1 for atan(1)
2-replacing f(x) for tan(x)
3-replacing dx for (1+tan(x)2)

Try use the replacement expressions in the table above for more examples of improper you have
in your book of calculus integrals and check the result.

Solving the Improper integral in the HP48G Series.

Now all we need is write the integral in the EQUATION WRITER	Long screenshot of the expression
and press EVAL to get the result.	Result of the integral

Solving Double and Triple Integrals

The steps to solve double and triple integrals are not difficult.
It is basically solve an integral 2 or 3 times.

All you need is write the expression in the EQUATION WRITER

Writing a Double Integral

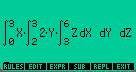Writing a Triple Integral

and press EVAL to solve.

Exercises

Use HP48 and the methods explained in this document to solve the following integrals:

Integral to solve	Result
a)	2/3 or 0.66666666666
b)	1/78635793761 or 1.27168551644E-11
c)	1/16 or 0.0625
d)	4/3 or 1.33333333333
e)	or 0.414213562373
f)	p/2 or 1,5707963268
g)	1/6 or 0.166666666666
h)	-( 1/6*A^6+A^2 +3*A) + (1/6*B^6 +B^2 +3*B)
i)	-SIN(R) + SIN(S)

---

---

Copyrights:

This document can be copied and freely distributed for educational purpose.
It is prohibited its reproduction for non-educational purpose.
Sell this document or use it for personal purpose is not permitted.
Exclude or modify the name of the author is not permitted. 
If you sell it to a friend, please, sell it for a just price.
Publishing in www sites is permitted since you don't modify this document
and give credits to Carlos Marangon.
Use it in classes or for learning is freely permitted.
This document is CAREWARE

I will maintain this document at

http://www.area48.com/integral
carlos@area48.com

---

---